Chap 4¶

约 1176 个字 78 张图片预计阅读时间 4 分钟

Sequential Circuits

引例

单一的R、S变量无法真正决定Q的状态，还要取决于内部的上一个状态。

Latch （锁存器）¶

每个门电路都有一个独立的电源，所以发光不是依靠输入的电源；（不是永动

两个稳定态，持续维持稳定状态，同时SR改变时状态发生改变

如果SR双置位，那么就会发生震荡，最后得到一个未知状态

亚稳态

给的信号时间过短，就会意外处于亚稳态，而亚稳态并不稳定也会造成未知状态

Synchronous Circuit¶

多与非* 的处理，让状态调整和C的一定频率同步，而不是SR改变就马上改变Q状态

D Latch¶

单输入的信号，锁存的信号就是D

Flip-Flops¶

Info

latch情况下会发生空翻现象
所以引入flip-flop

S-R Master-Slave Flip-Flop¶

Master 进行置位信号的采样
Slave 来决定Q的状态
两者工作在不同的时间片区

problem：1s catching

置位信号稍微有些抖动毛刺，都会产生错误信号且难以修正

D-Edge-Triggered¶

用D latch替换掉SR；因为只要在进入Slave前回到正确状态就行，关键就在高低电平转换的Edge
这个是主从类型的D-edge-triggered

这是带SR预置位的，正边沿触发

J-K Flip-Flop¶

JK就是升级版的SR，在保留了 00,01,10的功能前提下，将原来未知态的11变为了 \(Q(t+1)=\bar {Q(t)}\)

方程

特征方程：

\(Q(t+1)=J\bar Q+\bar KQ\)

激励方程：

\(J=Q(t+1)+Q(t)\\K=\bar{Q(t+1)}+\bar{Q(t)}\)

T Flip-Flop¶

相当于一个计数器，clk到edge就加一

方程

特征方程：

\(Q(t+1)=Q(t)\oplus T\)

激励方程：

\(T=Q(t)\oplus Q(t+1)\)

Flip-Flop Timing Parameters 时间参数¶

对于边缘触发器，必须给定一定时间的time to setup or hold，这样数据才能稳定存储，不然就会进入亚稳态

Sequential Circuit Analysis¶

四大方程¶

触发器的输入方程(flip-flop input equation) 输出方程（output equation）状态方程（next-state equation)激励方程（excitation equation）

表示触发器的D/SR/JK/T端和其他信号的逻辑关系

表示输出信号Y的逻辑

表示 \(Q(t+1)=F(Q(t),X,D)\)的逻辑

表示从 \(Q(t)到Q(t+1)\),D/SR/JK/T端需要的值 \(D=F(Q(t),X)\)
一般是两输入两输出（两个外部信号，两个内部信号）

Note

一共要分析三个方程

E.g.1

State Table¶

State Diagram¶

有向弧上表示了状态切换时的输入量；
然后输出结果有两种表示，也对应了两种类型：
- （Mealy type;Moore type）
Mealy type
- 输出与状态和输入都有关
- 有向弧上 input/output
Moore type
- 输出只与当前状态有关
- 有向弧上 input 状态圈里表示 output

Equivalent State(等价状态)¶

有相同的输入，输出，下一状态

E.g 2

TimingAnalysis of Sequential Circuits 时间分析¶

== "e.g1" - 只是从 input 到 output ：2个 xor

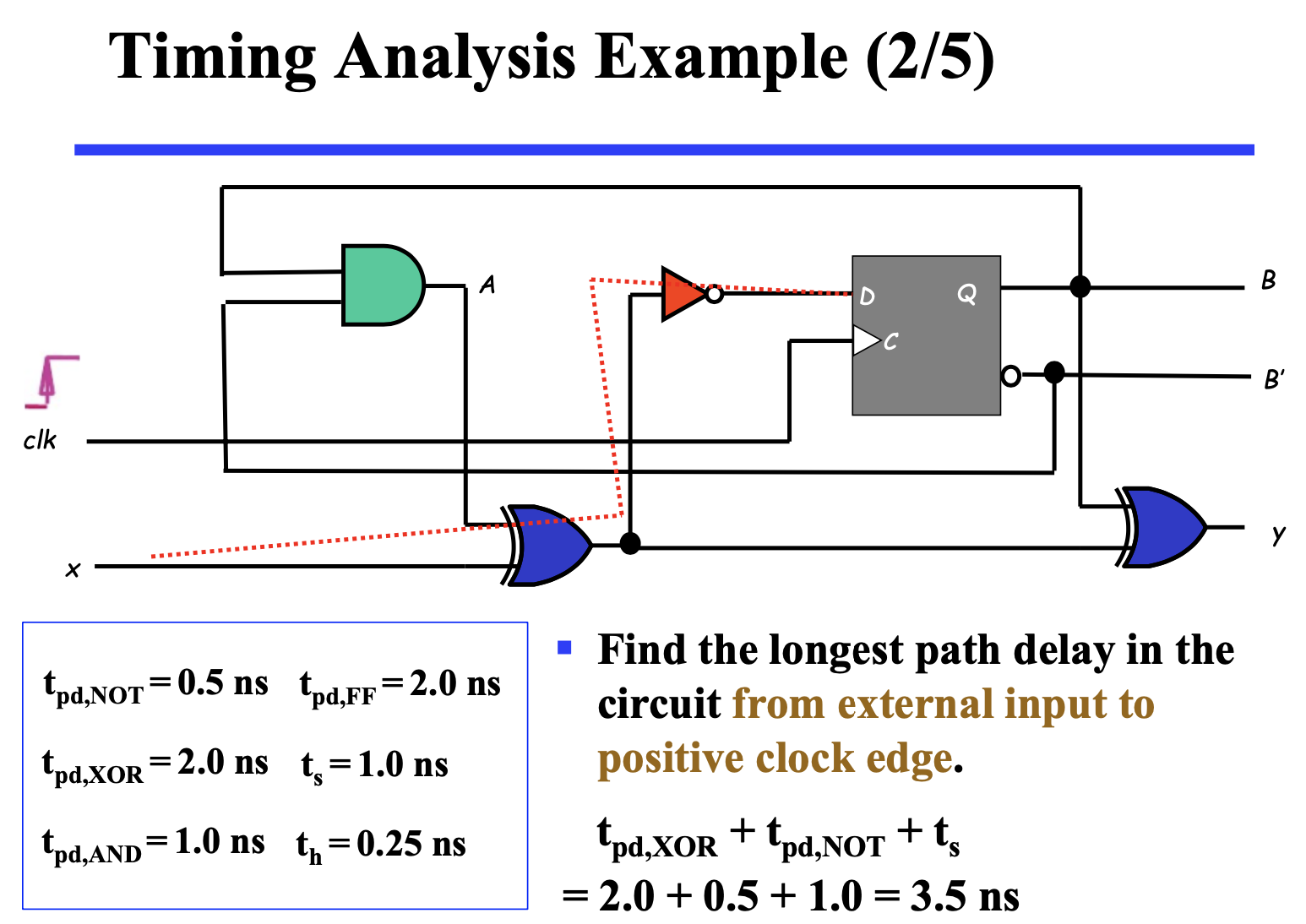
![Untitled](Logic%20and%20computer%20design%20fundamentals%20126e5290981e4d10ad7dab4e845bdd25/Untitled%20145.png)

e.g2e.g3e.g.4e.g.5

input 到 positive edge :xor+not+ts

positive edge to output : tpd+and+xor+xor

from positive to next positive : tpd+and+xor+not+ts

Maximum frequency : 就是从 clk edge到clk edge那段时间对应的频率

Method of Describing Sequential Analysis¶

电路设计也是三个方程！

难点在于什么是“状态” 能不能很好的抽象

Example 1101Example 1011-Moore型

初始状态设置成正确的序列

然后补全其余的state

接着根据状态图补全状态表

刚才的设计是 Mealy型
现在欲改为Moore型

去找输出都不变的就变更输出到状态里面去
（我们可以把输出藏在输入端或者输出端）

而对于无法处理的节点：新添节点
比如对于原图中的D节点

我们添加了E节点，同时理解E状态就是成功读取最后一个1之后的状态，所以再多一个1就到C，如果是0就到A

Simplification of State Table （状态表简化）¶

对于 Next State和Output 都相同的两个state 是等价，可以合并

Three cases of equivalent states
首先outputs一定要相同

Next States 相同
Next States interleaved 交错
Next States circulated 循环

Example 2 (modulo 3)Example unlimited sequences

对输出的理解不同，则model不同
Mealy：

Moore：
输出藏在了输入端

State Assignment Method¶

状态编码的方法
将状态进行编码，主要三种

Example 1

利用卡诺图化简得到input 和 output方程

BCDGrayone-hot

BCD编码 cost较高

Gray cost较低

Basic Flip-Flop Descriptors¶

特征方程：给定FF的信号，下一个Q(t+1)会如何变化
激励方程：给定Q(t)和Q(t+1)，需要如何的FF信号